1.Merge(归并)
把两个或多个有序的子序列合并为一个
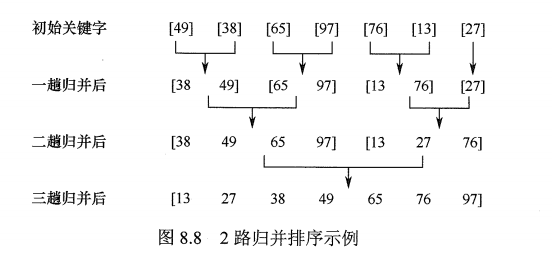
2路归并(二合一)
- n个元素2路归并排序,归并趟数 =
- 每趟归并的时间复杂度为O(n),则算法的时间复杂度为 O(nlogn)
- 空间复杂度:O(n),来自于辅助数组
k路归并(K合一)
m路归并,每选一个元素需要对比关键字 n-1次
2.算法思想
- 若low<high,则将序列从中间 mid=(low+high)/2分开
- 对左半部分 [low, mid] 递归进行归并排序
- 对有半部分 [mid+1, high] 递归进行归并排序
- 将左右两个有序序列Merge为一个
3.性能
- 空间复杂度:O(n)
- 时间复杂度:O(nlogn)
- 稳定性:稳定
4.代码
void merge(SqList& L, int low, int mid, int high) { // 辅助数组 ElemType* tmp = (ElemType*)malloc(sizeof(ElemType) * (L.length + 1)); // 表L中的元素,全部复制到tmp中 for (int k = low; k <= high; k++) tmp[k] = L.data[k]; int lowIndex = low; int highIndex = mid + 1; int indexLen = low; // 比较tmp的左右两段中的元素,将较小值复制到L中 while (lowIndex <= mid && highIndex <= high) { // 两个元素相等时,优先使用靠前的那个(稳定性) if (tmp[lowIndex] <= tmp[highIndex]) L.data[indexLen++] = tmp[lowIndex++]; else L.data[indexLen++] = tmp[highIndex++]; } // 若第一个表未检测完,复制 while(lowIndex <= mid) L.data[indexLen++] = tmp[lowIndex++]; // 若第二个表未检测完,复制 while (highIndex <= high) L.data[indexLen++] = tmp[highIndex++]; free(tmp); } void mergeSort(SqList& L, int low, int high) { if (low < high) { int mid = (low + high) / 2; mergeSort(L, low, mid); mergeSort(L, mid + 1, high); merge(L, low, mid, high); } }