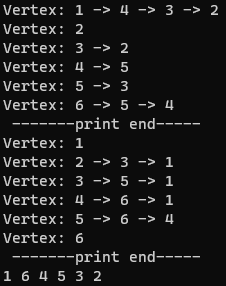
1.无向图连通分量
问题
求邻接表存储结构的无向图的连通分量的个数,并输出每个连通分量的顶点集
算法思想
- 用深度优先搜索,先从任意一个顶点开始进行深度优先搜索;
- 输出每一个遍历到的结点,搜索完后,连通分量个数增加1;
- 然后再从没有遍历过的顶点找一个出来进行DFS, 搜索完成后,连通分量个数加一;
- 直到所有的顶点都被遍历过。
代码
深度优先搜索
// 标记数组 bool visited[MAX_VERTEX] = { false }; void DFS(ALGraph* ALG, VertexType v) { // 访问标记 visited[v] = true; printf("->%d", v); // 获得头结点地址 ArcNode* pArcNode = ALG->vertices[v].firstArc; int neighborVertex = 0; // 重复取邻居结点 while (pArcNode != NULL) { neighborVertex = pArcNode->adjvex; // 重复取邻居结点,其存在弧结点 if (visited[neighborVertex] != true) DFS(ALG, neighborVertex); // 取下一个弧结点 pArcNode = pArcNode->next; } }
搜索连通分量
bool searchConnectedComponentGraph(ALGraph* ALG) { // 连通分量个数 int count = 0; for (int i = 1; i <= ALG->vexNum; i++) { if (visited[i] != true) { DFS(ALG, i); count++; // 连通分量个数加一 printf("\n"); } } printf("count:%d\n", count); return true; }
测试
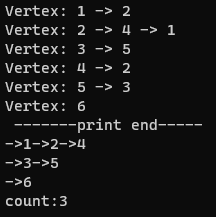
2.最短距离为K的路径
问题
求出无向连通图中距离顶点V0的最短距离长度为K的所有结点
算法思想
- 给顶点信息增加一个层信息,初始为0层;
- 使用BFS访问队列顶部元素的邻居结点;
- 邻居结点的层数等于出队列顶点层数加一;
- 当邻居结点层数等于k时,输出邻居结点,并不将邻居节点压入队列中;
- 若邻居结点层数不等于k,则将邻居结点压入队列中;
- 循环遍历。
代码
void computeShortestPathNodes(ALGraph* ALG, VertexType v0, int k) { // 初始化队列 Queue Q; initQueue(Q); visited[v0] = true; // 给顶点增加层信息 QueueElemType elem; elem.vex = v0; elem.level = 0; enQueue(Q, elem); while (!emptyQueue(Q)) { QueueElemType tmp; deQueue(Q, tmp); int level = tmp.level; ArcNode* pArcNode = ALG->vertices[tmp.vex].firstArc; // 访问邻居结点 while (pArcNode != NULL) { if (visited[pArcNode->adjvex] == false) { visited[pArcNode->adjvex] = true; // 将邻居结点加入队列 // 若层信息等于k,则输出结点,跳过后序循环 tmp.vex = pArcNode->adjvex; tmp.level = level + 1; if (tmp.level == k) { printf("%d ", tmp.vex); continue; } enQueue(Q, tmp); } pArcNode = pArcNode->next; } } }
3.图的根
问题
在有向图G中,如果r到G中的每个节点都有路径可达,则称结点r为G的根结点,判断图G是否有根,若有,打印所有的根结点
算法思想
- 设置一个全局变量,用来记录DFS访问结点的个数;
- 若DFS访问过结点的个数为顶点数,则此顶点为根,将根打印即可。
代码
int nodeCount = 0; // 深度优先遍历所有根结点 void DFSRoot(ALGraph ALG, VertexType v) { visited[v] = true; // 访问结点数量加一 nodeCount++; ArcNode* pArcNode = ALG.vertices[v].firstArc; while (pArcNode != NULL) { if (visited[pArcNode->adjvex] != true) DFSRoot(ALG, pArcNode->adjvex); pArcNode = pArcNode->next; } }
int graphRootDFS(ALGraph ALG) { // 初始标记数组 for (int v = 1; v <= ALG.vexNum; v++) { visited[v] = false; } // 依次访问每一个节点,查找是否是根结点 for (int i = 1; i <= ALG.vexNum; i++) { DFSRoot(ALG, i); // 如果等于顶点数目,则是根结点 if (nodeCount == ALG.vexNum) printf("root: %d\n", i); // 将访问数组、全局计数变量清除 for (int v = 1; v <= ALG.vexNum; v++) { visited[v] = false; } nodeCount = 0; } }
4.BFS改进
问题
图的D遍历类似于BFS,不同之处在于使用栈代替BFS中的队列,入队操作改为入栈操作,即当作一个顶点的所有邻接点被搜索之后,下一个搜索出发点应该是最近入栈(栈顶)的顶点。用邻接表做储存结构,编写D遍历算法。
算法思想
将BFS中的队列换为栈即可。
代码
从某顶点开始D遍历
void DBFS(ALGraph* ALG, VertexType v) { Stack S; initStack(S); // 压入栈时,要标记,防止重复 visited[v] = true; push(S, v); // 栈不为空,循环出栈 while (!emptyStack(S)) { StackType elem; pop(S, elem); printf("->%d ", elem); ArcNode* pArcNode = ALG->vertices[elem].firstArc; while (pArcNode != NULL) { if (visited[pArcNode->adjvex] != true) { visited[pArcNode->adjvex] = true; push(S, pArcNode->adjvex); } pArcNode = pArcNode->next; } } }
D遍历
void DBFSTraverse(ALGraph* ALG) { for (int i = 1; i <= ALG->vexNum; i++) { visited[i] = false; } for (int i = 1; i <= ALG->vexNum; i++) { if (visited[i] != true) { DBFS(ALG, i); printf("\n"); } } }
5.图G顶点编号
问题
设G=(V, E)是一个以邻接表存储的有向无环图,编写一个给图G中每一个顶点赋一个整型序号的算法,并满足以下条件:从顶点i到顶点j有一条弧,则应使i<j。
算法思想
- “有向无环”,优先考虑拓扑排序
- DFS逆拓扑排序实现,需要辅助数组或栈
- BFS 拓扑排序,不需要辅助空间
代码
访问标记数组和全局变量
// 数据标记,大于0,则给相应顶点赋了序号 int visitNum[MAX_VERTEX] = { 0 }; int globalCount = 100; // 很大的数,给顶点赋值
从一个顶点DFS遍历,在顶点退出时,给顶点序号
void DFSSort(ALGraph* ALG, VertexType v) { visitNum[v] = 1; ArcNode* pArcNode = ALG->vertices[v].firstArc; while (pArcNode != NULL) { if (visitNum[pArcNode->adjvex] == 0) DFSSort(ALG, pArcNode->adjvex); pArcNode = pArcNode->next; } visitNum[v] = globalCount--; }
分别遍历每一个,并打印序号
void orderVertexTopo(ALGraph* ALG) { for (int i = 1; i <= ALG->vexNum; i++) { visitNum[i] = 0; } for (int i = 1; i <= ALG->vexNum; i++) { if (visitNum[i] == 0) DFSSort(ALG, i); } for (int i = 1; i <= ALG->vexNum; i++) { printf("%d ", visitNum[i]); } printf("\n"); }
6.逆邻接表拓扑排序
问题
在逆邻接表上实现拓扑排序算法
算法思想
逆邻接表的DFS与邻接表的BFS拓扑排序的结果时一样的
邻接表的DFS与逆邻接表的DFS是逆序的
邻接表的DFS与邻接表的BFS是逆序的
代码
标记、数组定义
bool visited[MAX_VERTEX] = { false }; VertexType path[MAX_VERTEX]; int pathLength = 0;
从某一顶点拓扑排序
void invALGDFS(ALGraph* ALG, VertexType v) { visited[v] = true; ArcNode* pArcNode = ALG->vertices[v].first; while (pArcNode != NULL) { if (visited[pArcNode->adjvex] != true) invALGDFS(ALG, pArcNode->adjvex); pArcNode = pArcNode->next; } // 退出时,将顶点存到数组中 path[pathLength++] = v; }
全部顶点拓扑排序
void invALGTopoSort(ALGraph* ALG) { // 标记数组为false for (int i = 1; i <= ALG->vexnum; i++) { visited[i] = false; } // 逆邻接表DFS拓扑排序 for (int i = 1; i <= ALG->vexnum; i++) { if (visited[i] != true) invALGDFS(ALG, i); } for (int i = 0; i < pathLength; i++) { printf("%d ", path[i]); } printf("\n"); }
测试